corpus = np.array([0, 1, 2, 3, 4, 1, 2, 3])
power = 0.75
sample_size = 2
sampler = UnigramSampler(corpus, power, sample_size)
target = np.array([1, 3, 0])
negative_sample = sampler.get_negative_sample(target)
print(negative_sample)
# [[0 3]
# [2 1]
# [2 1]]앞서 CBOW 모델은 말뭉치에 포함된 어휘 수가 많아지면 계산량이 커져 계산 시간이 너무 오래 걸린다. 이번 장에서는 word2vec의 속도 개선을 Embedding 계층과 Negative Sampling loss로 개선할 예정이다.
4.1 word2vec 개선 I - Embedding 계층
- CBOW 모델은 단어 2개를 맥락으로 사용해, 하나의 단어(타깃)을 추측한다. 이때 거대한 말뭉치를 넣게 되면, 입력층과 출력층에는 그 vocab 만큼의 뉴런이 존재하게 된다.(sparse, one-hot encoding vector -> 원핫 표현의 벡터 크기가 커지게 됨.)
- 그 경우 (1) 입력층의 원핫 표현과 가중치 행렬 $W_{in}$의 곱 계산, (2) 은닉층과 가중치 행렬 $W_{out}$의 곱 및 Softmax 계층의 계산 이 두 계산에서 병목이 일어난다. 이를 각각 Embedding, negative sampling loss를 도입하는 것으로써 해결한다.
4.1.1 Embedding 계층

- 어휘 수가 100만개, 은닉층 뉴런이 100개라면 MatMul 계층의 행렬 곱은 위 그림과 같이 표현된다.
- 그림을 보면 알 수 있듯, 위에서 결국 수행하는 것은 단지 행렬의 특정 행을 추출하는 것 뿐임. 따라서 원핫 변환과 MatMul 계층의 행렬 곱 계산은 사실상 필요가 없다. 이를 Embedding 계층을 만들어보며 살펴보자.
4.1.2 Embedding 계층 구현

class Embedding:
def __init__(self, W):
self.params = [W]
self.grads = [np.zeros_like(W)]
self.idx = None
def forward(self, idx):
W, = self.params
self.idx = idx
out = W[idx]
return out
def backward(self, dout):
dW, = self.grads
dW[...] = 0
dW[self.idx] = dout
return None- forward() : 가중치 W의 특정 행을 추출할 뿐임.
- backward() : 앞 층(출력 측 층)으로부터 전해진 기울기를 다음 층(입력 측 층)으로 그대로 흘려주면 됨. 다만, 앞 층에서 전해진 기울기를 가중치 기울기 dW의 특정 행(idx번째 행)에 설정한다. 즉, 가중치 기울기 dW를 꺼낸 다음, dW의 원소를 0으로 덮어쓰고 앞 층에서 전해진 기울기 dout을 idx번째 행에 할당한다.
- WARNING : 결국 가중치 W를 갱신하는게 목표이므로 dW 행렬을 만들 필요 없이 갱신하려는 행 번호(idx)와 그 기울기(dout)를 따로 저장하면 가중치 W의 특정 행만 갱신할 수 있다. 다만 여기에서는 이미 구현해 둔 갱신용 클래스 (Optimizer)와 조합해 사용하는 것을 고려해 지금처럼 구현되어있다.
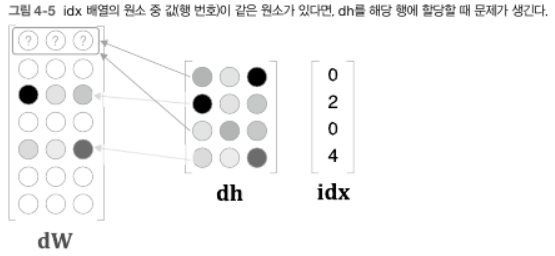
- 위 backward() 구현의 문제 : idx의 원소가 중복될 경우 먼저 쓰여진 값을 덮어쓰는 문제가 있음. 이 중복 문제를 해결하려면 '할당'이 아니라 '더하기'를 해야함. 즉, dh의 각 행의 값을 dW의 해당 행에 더해준다. 이를 올바르게 구현하면 다음과 같다:
def backward(self, dout):
dW, = self.grads
dW[...] = 0
for i, word_id in enumerate(self.idx):
dW[word_id] += dout[i]
# or
# np.add.at(dW, self.idx, dout)
return None4.2 word2vec 개선 II - Negative Sampling
- 은닉층과 $W_{out}$ 행렬곱과 softmax 계층의 계산 병목을 해소하는 방법으로 네거티브 샘플링 기법을 사용한다. 이럴 경우 어휘가 아무리 많아져도 계산량을 낮은 수준에서 억제할 수 있다.
4.2.1 은닉층 이후 계산의 문제점

- 매우 큰 행렬 곱 계산은 시간과 메모리가 많이 필요하기 때문에 이 행렬 곱을 '가볍게' 만들어야 하며 어휘가 많아지면 softmax의 계산량도 증가한다. ($y_k = \frac{exp(s_k)}{\sum_{i=1}^{1000000} exp(s_i)}$이기 때문에 분모에서 exp 계산을 100만 번 수행해야 함.)
4.2.2 다중 분류에서 이진 분류로
- 네거티브 샘플링의 핵심 아이디어는 '다중 분류'를 '이진 분류'로 근사하는 데에 있다.
- 이렇게 하면 출력층에는 뉴런을 하나만 준비하면 된다. 즉, 출력층의 타깃 단어만의 점수를 구하는 신경망을 생각하면 된다.


- 출력 층의 뉴런을 하나로 둠으로써 은닉층과 출력 층의 가중치 행렬의 내적은 'say'에 해당하는 열(단어 벡터)만을 추출하고, 그 벡터와 은닉층 뉴런과의 내적을 계산하면 최종 점수를 얻을 수 있다. (출력 층의 가중치 $W_{out}$의 각 열 벡터는 각 단어 id의 벡터가 저장되어있음.)
4.2.3 시그모이드 함수와 교차 엔트로피 오차
- 이진 분류 : score에 sigmoid 함수를 적용해 확률로 변환하고, 교차 엔트로피 오차를 사용해 손실함수를 계산한다. (다중분류 - 소프트맥스, 교차 엔트로피 loss, 이진분류 - 시그모이드, 교차 엔트로피 loss)
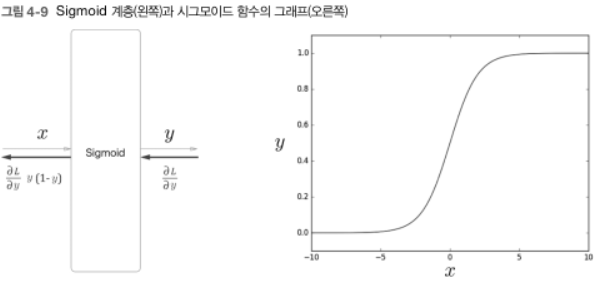
- $y = \frac{1}{1+exp(-x)}$로, 입력 값(x)를 0에서 1 사이의 실수로 변환하기 때문에 출력 y를 '확률'로 해석 가능하다.
- Loss : $L = -(tlogy + (1-t)log(1-y))$ 즉, $t=1$이면 $-log y$가, $t = 0$이면 $-log(1-y)$가 됨. 따라서 Sigmoid 계층과 Cross Entropy Error 계층의 계산 그래프는 다음과 같다 :

- 역전파의 $y-t$ 값은 곧 신경망이 출력한 확률과 정답 레이블의 차이가 된다. 오차가 앞 계층으로 흘러가므로 오차가 크면 '크게', 오차가 작으면 '작게' 학습하게 된다
4.2.4 다중 분류에서 이진 분류로 (구현)
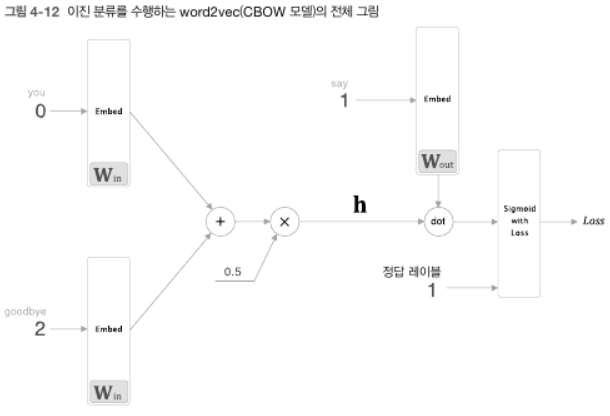
- 결국 은닉층 뉴런 $\mathbf{h}$와 출력 층의 가중치 $W_{out}$에서 'say'에 해당하는 열 단어벡터와의 내적을 계산한 뒤에 그 출력을 Sigmoid with Loss 계층에 입력해 최종손실을 얻음!
class EmbeddingDot:
def __init__(self, W):
self.embed = Embedding(W)
self.params = self.embed.params
self.grads = self.embed.grads
self.cache = None
def forward(self, h, idx):
target_W = self.embed.forward(idx)
out = np.sum(target_W * h, axis = 1)
self.cache = (h, target_W)
return out
def backward(self, dout):
h, target_W = self.cache
dout = dout.reshape(dout.size, 1)
dout = dout.reshape(dout.shape[0], 1)
dtarget_W = dout * h
self.embed.backward(dtarget_W)
dh = dout * target_W
return dh- forward(h, idx) : 인수로 은닉층 뉴런(h)와 단어 Id의 넘파이 배열(idx)을 받는다. 우선 Embedding 계층의 forward(idx)를 호출 한 다음 내적을 계산한다.
4.5.2 네거티브 샘플링
- 궁극적으로 원하는 목표 : 긍정적 예('say')에 대해서는 Sigmoid 계층의 출력을 1에 가깝게 만들고, 부정적 예('say' 이외의 단어)에 대해서는 Sigmoid 계층의 출력을 0에 가깝게 만드는 것.
- 하지만 모든 부정적 예를 대상으로 해 이진 분류를 학습시키면 어휘 수 증가에 대처할 수 없다. 따라서 근사적 해법으로 적은 수의 부정적 예를 샘플링해 사용한다. 이를 '네거티브 샘플링'이라 한다.
- 네거티브 샘플링(Negative Sampling) : 긍정적 예를 타깃으로 한 경우의 손실을 구함과 동시에 부정적 예를 몇 개 샘플링(선별)하여, 그 부정적 예에 대해서도 손실을 구하고 각 손실을 더한 값을 최종 손실로 사용한다.

- 긍정적 예에 대해서는 sigmoid with loss 계층에 정답 lable로 1을, 부정적 예에 대해서는 0을 입력해야 함을 주의하자.
4.2.6 네거티브 샘플링의 샘플링 기법
- 말뭉치의 통계 데이터를 기초로 네거티브 샘플링을 진행한다. 구체적으로는, 자주 등장하는 단어를 많이 추출하고 드물게 등장하는 단어를 적게 추출한다.
- 즉, 말뭉치에서 각 단어의 출현 횟수를 구해 '확률분포'로 나타낸 뒤 그 분포대로 단어를 샘플링한다.
import numpy as np
words = ['you', 'say', 'goodbye', 'I', 'hello', '.']
print(np.random.choice(words, size=5, replace = False)) # 중복 없음
# ['you' 'goodbye' 'say' 'hello.' 'goodbye']
p = [0.5, 0.1, 0.05, 0.2, 0.05, 0.1]
print(np.random.choice(words, p=p))
# you- word2vec 네거티브 샘플링에서는 출현 확률이 낮은 단어의 확율을 조금 올리기 위해 기본 확률분포에 0.75를 제곱하라고 권고한다. $$P'(w_i) = \frac{P(w_i)^{0.75}}{\sum_{j}^n P(w_j)^0.75}$$
- 네거티브 샘플링 클래스를 UnigramSampler로 구현한 코드가 다음과 같다.
import collections
class UnigramSampler:
def __init__(self, corpus, power, sample_size):
self.sample_size = sample_size
self.vocab_size = None
self.word_p = None
counts = collections.Counter()
for word_id in corpus:
counts[word_id] += 1
vocab_size = len(counts)
self.vocab_size = vocab_size
self.word_p = np.zeros(vocab_size)
for i in range(vocab_size):
self.word_p[i] = counts[i]
self.word_p = np.power(self.word_p, power)
self.word_p /= np.sum(self.word_p)
def get_negative_sample(self, target):
batch_size = target.shape[0]
if not GPU:
negative_sample = np.zeros((batch_size, self.sample_size), dtype=np.int32)
for i in range(batch_size):
p = self.word_p.copy()
target_idx = target[i]
p[target_idx] = 0
p /= p.sum()
negative_sample[i, :] = np.random.choice(self.vocab_size, size=self.sample_size, replace=False, p=p)
else:
# GPU계산시에는 속도를 우선한다.
# 부정적 예에 타깃이 포함될 수 있다.
negative_sample = np.random.choice(self.vocab_size, size=(batch_size, self.sample_size),
replace=True, p=self.word_p)
return negative_samplecorpus = np.array([0, 1, 2, 3, 4, 1, 2, 3])
power = 0.75
sample_size = 2
sampler = UnigramSampler(corpus, power, sample_size)
target = np.array([1, 3, 0])
negative_sample = sampler.get_negative_sample(target)
print(negative_sample)
# [[0 3]
# [2 1]
# [2 1]]- 미니 배치로 3개의 긍정적 예 [1, 3, 0]을 입력으로 넣어, 각각 부정적 예를 2개씩 샘플링 한 결과이다.
4.2.7 네거티브 샘플링 구현
class SigmoidWithLoss:
def __init__(self):
self.params, self.grads = [], []
self.loss = None
self.y = None # sigmoid의 출력
self.t = None # 정답 데이터
def forward(self, x, t):
self.t = t
self.y = 1 / (1 + np.exp(-x))
self.loss = cross_entropy_error(np.c_[1 - self.y, self.y], self.t)
return self.loss
def backward(self, dout=1):
batch_size = self.t.shape[0]
dx = (self.y - self.t) * dout / batch_size
return dx
class NegativeSamplingLoss:
def __init__(self, W, corpus, power=0.75, sample_size=5):
self.sample_size = sample_size
self.sampler = UnigramSampler(corpus, power, sample_size)
self.loss_layers = [SigmoidWithLoss() for _ in range(sample_size + 1)]
self.embed_dot_layers = [EmbeddingDot(W) for _ in range(sample_size + 1)]
self.params, self.grads = [], []
for layer in self.embed_dot_layers:
self.params += layer.params
self.grads += layer.grads
def forward(self, h, target):
batch_size = target.shape[0] # mini-batch
negative_sample = self.sampler.get_negative_sample(target)
# 긍정적 예 순전파
score = self.embed_dot_layers[0].forward(h, target)
correct_label = np.ones(batch_size, dtype=np.int32)
loss = self.loss_layers[0].forward(score, correct_label)
# 부정적 예 순전파
negative_label = np.zeros(batch_size, dtype=np.int32)
for i in range(self.sample_size):
negative_target = negative_sample[:, i]
score = self.embed_dot_layers[1 + i].forward(h, negative_target)
loss += self.loss_layers[1 + i].forward(score, negative_label)
return loss
def backward(self, dout=1):
dh = 0
for l0, l1 in zip(self.loss_layers, self.embed_dot_layers):
dscore = l0.backward(dout)
dh += l1.backward(dscore)
return dh- __init__ : 출력 측 가중치를 나타내는 W, corpus, power, 부정적 예의 샘플링 횟수인 sample_size, UnigramSampler 등을 저장한다. 인스턴스 변수인 loss_layers와 embed_dot_layers 두 리스트에 sample_size + 1만큼의 계층을 생성하는 이유는 긍정적 예를 다루는 계층 1개, 부정적 예츨 다루는 계층 sample_size 개 만큼 필요하기 때문이다. 정확히는 0번째 계층 loss_layer[0]과 embed_dot_layers[0]이 긍정적 예를 다루는 계층이다.
- forward(h, target) : 은닉층 뉴런 h와 긍정적 예의 타깃을 뜻하는 target을 받음. 우선 self.sampler로 부정적 예를 샘플링해 negative_sample에 저장한다. 그 뒤 긍정적 예 / 부정적 예 각각에 대해 순전파를 수행해 손실을 더한다.
구체적으로는 Embedding Dot 계층의 forward 점수를 구하고, 이어서 이 점수와 레이블을 Sigmoid With Loss 계층으로 흘려 손실을 구한다. 이때 긍정적 예의 정답 label = "1", 부정적 예의 정답 label = "0"이다. - backward : 순전파의 역순으로 각 계층의 backward()를 호출하면 된다.
4.3 개선판 word2vec 학습
4.3.1 CBOW 모델 구현
- Embedding 계층과 Negative Sampling Loss 계층을 적용하고, 맥락의 윈도우 크기를 조절할 수 있도록 확장함.

class CBOW:
def __init__(self, vocab_size, hidden_size, window_size, corpus):
V, H = vocab_size, hidden_size
# 가중치 초기화
W_in = 0.01 * np.random.randn(V, H).astype('f')
W_out = 0.01 * np.random.randn(V, H).astype('f')
# 계층 생성
self.in_layers = []
for i in range(2 * window_size):
layer = Embedding(W_in)
self.in_layers.append(layer)
self.ns_loss = NegativeSamplingLoss(W_out, corpus, power=0.75, sample_size = 5)
# 모든 가중치와 기울기를 배열에 모은다.
layers = self.in_layers + [self.ns_loss]
self.params, self.grads = [], []
for layer in layers:
self.params += layer.params
self.grads += layer.grads
# 인스턴스 변수에 단어의 분산 표현을 저장한다.
self.word_vecs = W_in
def forward(self, contexts, target):
h = 0
for i, layer in enumerate(self.in_layers):
h += layer.forward(contexts[:, 1])
h *= 1 / len(self.in_layers)
loss = self.ns_loss.forward(h, target)
return loss
def backward(self, dout = 1):
dout = self.ns_loss.backward(dout)
dout *= 1 / len(self.in_layers)
for layer in self.in_layers:
layer.backward(dout)
return None- __init__ : vocab_size(어휘 수), hidden_size(은닉층의 뉴런 수), corpus(단어 ID 목록), window_size(맥락의 크기)를 받음. 가중치 초기화 이후 Embedding 계층을 2*window_size만큼 생성하고 Negative Sampling Loss 계층을 생성한다.
- forward() : 각 계층의 순전파, 역전파를 적절한 순서로 호출한다. 단, forward(contexts, target) 메서드가 인수로 받는 맥락과 타깃이 단어 ID이다.
4.3.2 CBOW 모델 학습 코드
window_size = 5
hidden_size = 100
batch_size = 100
max_epoch = 10
GPU = False
# read data
corpus, word_to_id, id_to_word = load_data('train')
vocab_size = len(word_to_id)
contexts, target = create_contexts_target(corpus, window_size)
if GPU:
contexts, target = to_gpu(contexts), to_gpu(target)
# 모델 등 생성
model = CBOW(vocab_size, hidden_size, window_size, corpus)
optimizer = Adam()
trainer = Trainer(model, optimizer)
# 학습 시작
trainer.fit(contexts, target, max_epoch, batch_size)
trainer.plot()
# 나중에 사용할 수 있도록 필요한 데이터 저장
word_vecs = model.word_vecs4.3.3 CBOW 모델 평가
pkl_file = 'cbow_params.pkl'
# pkl_file = 'skipgram_params.pkl'
with open(pkl_file, 'rb') as f:
params = pickle.load(f)
word_vecs = params['word_vecs']
word_to_id = params['word_to_id']
id_to_word = params['id_to_word']
# 가장 비슷한(most similar) 단어 뽑기
querys = ['you', 'year', 'car', 'toyota']
for query in querys:
most_similar(query, word_to_id, id_to_word, word_vecs, top=5)- 실제로 실행해 보면 'you' 인칭대명사와 가장 비슷한 단어로 'i', 'we' 등이 나오는 것을 확인 가능하다.
- Word2Vec으로 얻은 단어의 분산 표현은 비슷한 단어를 가까이 모아줌과 동시에 더 복잡한 패턴을 파악한다.
- 유추 문제(비유 문제) : ex) king - man + woman = queen. 즉 단어 벡터 공간에서 man -> woman 벡터와 king -> ? 벡터가 가능한 한 가까워지는 단어를 찾을 수 있게 되는 것이다.
- 아래 analogy() 함수를 사용하면 이런 유추 문제를 처리할 수 있음
def analogy(a, b, c, word_to_id, id_to_word, word_matrix, top=5, answer=None):
for word in (a, b, c):
if word not in word_to_id:
print('%s(을)를 찾을 수 없습니다.' % word)
return
print('\n[analogy] ' + a + ':' + b + ' = ' + c + ':?')
a_vec, b_vec, c_vec = word_matrix[word_to_id[a]], word_matrix[word_to_id[b]], word_matrix[word_to_id[c]]
query_vec = b_vec - a_vec + c_vec
query_vec = normalize(query_vec)
similarity = np.dot(word_matrix, query_vec)
if answer is not None:
print("==>" + answer + ":" + str(np.dot(word_matrix[word_to_id[answer]], query_vec)))
count = 0
for i in (-1 * similarity).argsort():
if np.isnan(similarity[i]):
continue
if id_to_word[i] in (a, b, c):
continue
print(' {0}: {1}'.format(id_to_word[i], similarity[i]))
count += 1
if count >= top:
return
# 유추(analogy) 작업
print('-'*50)
analogy('king', 'man', 'queen', word_to_id, id_to_word, word_vecs)
analogy('take', 'took', 'go', word_to_id, id_to_word, word_vecs)
analogy('car', 'cars', 'child', word_to_id, id_to_word, word_vecs)
analogy('good', 'better', 'bad', word_to_id, id_to_word, word_vecs)
- 이처럼 word2vec으로 얻은 단어의 분산 표현을 사용하면, 단어의 단순한 의미 뿐 만 아니라 문법적 패턴도 파악할 수 있다.
4.4 Word2Vec 남은 주제
4.4.1 word2vec을 사용한 애플리케이션의 예
- 자연어 처리 분야에서 단어의 분산 표현이 중요한 이유는 전이학습(transfer learning)에 있다.
- 큰 말뭉치로 학습을 끝낸 후 그 분산표현을 텍스트 분류, 문서 클러스터링, 품사 태깅 등의 자연어 처리 작업에 활용할 수 있다.
- 단어의 분산 표현은 단어와 문장을 고정 길이 벡터로 변환할 수 있다는 장점도 존재함. (단어의 분산표현 벡터 합으로 문장을 표현하는 bag-of-words 방법. 단어의 순서를 고려하지 않음.)
- 자연어를 고정 길이 벡터로 변환함으로써 일반적인 머신 러닝 기법이 적용 가능해진다.
4.4.2 단어 벡터 평가 방법
- 단어의 분산 표현을 만드는 시스템과 분류하는 (downstream-task) 시스템의 학습은 따로 수행할 수도 있다. 예를 들면 단어의 분산 표현의 차원 수가 최종 정확도에 어떤 영향을 주는지 조사하려면, 우선 단어의 분산 표현을 학습하고, 그 분산 표현을 사용하여 또 하나의 머신러닝 시스템을 학습시켜야 한다.
- 그래서 단어의 분산 표현의 우수성을 실제 애플리케이션과는 분리해 평가하는 것이 일반적인데, 이때 주로 사용되는 평가 척도는 단어의 '유사성'이나 '유추 문제'를 활용한 평가이다.
- 유사성 평가 : 사람이 작성한 단어 유사도를 검증 세트를 사용해 평가하는 것이 일반적임. ex) 유사도를 0~10 사이로 점수화하면 'cat'과 'animal'의 유사도는 8점 등 사람이 단어 사이의 유사한 정도를 규정하고 이와 word2vec에 의한 코사인 유사도 점수를 비교해 그 상관성을 보는 방법
- 유추 문제를 활용한 평가 : 'king : queen = man : ?'과 같은 유추 문제를 출제하고 정답률로 단어의 분산표현의 우수성을 측정함.
- 다만 단어의 분산 표현의 우수함이 애플리케이션에 얼마나 기여하는지는 그 애플리케이션 종류나 말뭉치의 내용 등 다루는 문제 상황에 따라 다르다.
4.5 정리
- Embedding 계층은 단어의 분산 표현을 담고 있으면서, 순전파 시 지정한 단어 ID의 벡터를 추출한다.
- word2vec은 어휘 수의 증가에 비례하여 계산량도 증가하므로, 근사치로 계산하는 빠른 기법을 사용하면 좋다.
- 네거티브 샘플링은 부정적 예를 몇 개 샘플링하는 기법으로, 이를 이용하면 다중 분류를 이진분류처럼 취급할 수 있다.
- word2vec으로 얻은 단어의 분산 표현에는 단어의 의미가 녹아들어 있으며, 비슷한 맥락에서 사용되는 단어는 단어 벡터 공간에서 가까이 위치한다.
- word2vec의 단어의 분산 표현을 이용하면 유추 문제를 벡터의 덧셈과 뺄셈으로 풀 수 있게 된다.
- word2vec은 전이학습 측면에서 특히 중요하며, 그 단어의 분산 표현은 다양한 자연어 처리 작업에 이용할 수 있다.
'Deep Learning' 카테고리의 다른 글
| [밑바닥부터 시작하는 딥러닝2] Chapter 6. 게이트가 추가된 RNN (9) | 2024.07.22 |
|---|---|
| [밑바닥부터 시작하는 딥러닝2] Chapter 5. 순환 신경망(RNN) (0) | 2024.07.15 |
| [밑바닥부터 시작하는 딥러닝2] Chapter 3. Word2Vec (1) | 2024.07.02 |
| [밑바닥부터 시작하는 딥러닝2] Chapter 2. 자연어와 단어의 분산 표현 (3) | 2024.06.24 |
| [밑바닥부터 시작하는 딥러닝2] Chapter 1. 신경망 복습 (0) | 2024.06.18 |



