본 게시글은 Stanford CS224N NLP with Deep Learning 강의를 들으면서 내용을 정리한 것입니다.
Word2Vec
1. Review : Main Idea of word2vec
- 거대한 corpus가 존재하고, 각 corpus 내 단어 position으로부터 center word를 둘러싸고 있는 다른 word를 예측하는 방법.
- random word vector부터 시작해서 전체 corpus 내 모든 단어들을 대상으로 계산됨.
- word vector를 활용해서 주변 단어들을 예측하고자 함. $P(o|c) = \frac{exp(u_0^T v_c)}{\sum_{w \in V} exp(u)w^T v_c)}$

- Learning : 주변의 단어들을 더 잘 예측할 수 있도록 vector를 업데이트. 또한 word의 space에서의 유사성과 유의미한 방향을 반영하도록 학습된다.
- Word2Vec은 유사한 단어들은 단어공간 하에서 비슷하게 위치하도록 objective function을 최대화한다.
2. Optimization : Gradient Descent
(1) Gradient Descent - Q) 어떻게 "좋은" word vector를 얻을 수 있을까?
- random word vector로부터 시작한다.
- Idea : 현재 value $\theta$로부터 Minimize 해야 하는 cost function $J(\theta)$의 gradient를 계산하고, 그 gradient의 반대 방향으로 (negative gradient) 조금씩 step을 옮겨가며 반복해서 계산하는 방식이다.
- 이때 parameter로써 step size를 결정하는 것이 중요. 너무 작으면 global minimum 계산에 오래걸리고, 너무 크면 diverge하거나 bouncing 때문에 minimum 찾는 데 더 오래 걸릴 수 있음.
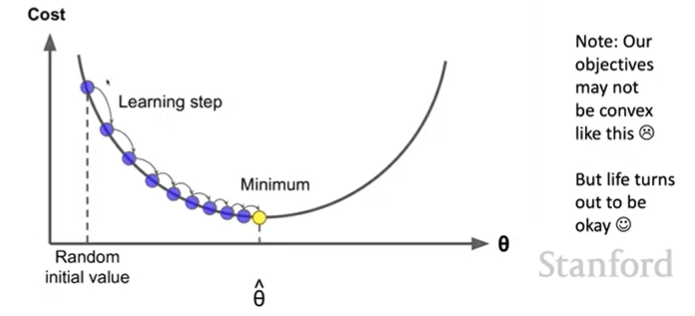
- Update Equation : $\theta^{new} = \theta^{old} - \alpha \nabla_\theta J(\theta)$, for $\alpha$ = step size or learning rate.
(2) Stochastic Gradient Descent
- Problem : $J(\theta)$는 corpus 내 모든 window에 관한 함수임. 따라서 이의 gradient를 계산하기 위해서는 계산량이 매우 많음!
- Solution : SGD(Stochastic Gradient Descent) - small batch마다 반복적으로 학습을 진행하는 것
- algorithm :
while True: window = sample_window(corpus) theta_grad = evaluate_gradient(J, window, theta) theta = theta - alpha * theta_grad - performance heck! 복잡한 network에선 더 잘 작동한다는 연구결과도 존재.
- SGD update를 하나의 sample window에서 수행한다고 하면, 최대 $2m+1$ 단어들에 대해서만 수행하기 때문에 매우 sparse한 $\nabla_\theta J_t(\theta)$를 갖게된다.
3. Word2Vec Algorithm Family
Two Model Variants
- Skip-grams (SG) : center word가 주어진 상태로 context("outside") words를 예측 (Position Independent - 각 단어들이 center인지, 앞인지, 뒤인지는 상관 X)
- Continuous Bag of Words (CBOW) : bag of context words로 center word를 예측.
Additional Efficiency in Training
- Naive Softmax : $P(o|c) = \frac{exp(u_o^T v_c)}{\sum_{w \in V} exp(u)w^T v_c)}$ 분모 계산이 매우 expansive. 모든 vocabulary에 대해 dot product를 계산해야 하기 때문.
Negative Sampling
- Main Idea : naive softmax 대신 binary logistic regression model을 (true center word, true context word) vs (true center word, random sample words) pair에 대해 학습시키는 아이디어.
- "Distributed Representations of Words and Phrases and their Compositionality" (Mikolov et al. 2013)
Maximize Objective function : $J_t(\theta)=\log \sigma\left(u_o^T v_c\right)+\sum_{i=1}^k \mathbb{E}_{j \sim P(w)}\left[\log \sigma\left(-u_j^T v_c\right)\right]$, and $J(\theta) = \frac{1}{T}\sum_{t=1}^T J_t(\theta)$ - $ \log \sigma\left(u_o^T v_c\right) $ : softmax 사용 대신 logistic(sigmoid) function을 활용 $\sigma(x) = \frac{1}{1 + e^{-x}}$ 함으로써 center word와 outsize word 간의 dot product가 커질 경우 1에 가까운 값을 갖도록 설정.
- $\sum_{i=1}^k \mathbb{E}_{j \sim P(w)}\left[\log \sigma\left(-u_j^T v_c\right)\right]$ : center word와 randomly 뽑힌 단어 간의 dot product는 작게 유지되도록 objective function을 설정.
- 즉, 동시에 등장하는 두 단어들의 probability는 최대화하고 nosiy한 단어들의 probability는 최소화한다고 보면 됨.
- 다시 수식으로 정리하자면,
$J_{\text {neg-sample }}\left(\boldsymbol{u}_o, \boldsymbol{v}_c, U\right)=-\log \sigma\left(\boldsymbol{u}_o^T \boldsymbol{v}_c\right)-\sum_{k \in\{K \text { sampled indices }\}} \log \sigma\left(-\boldsymbol{u}_k^T \boldsymbol{v}_c\right)$ - 위의 negative sample은 무엇으로부터 뽑을까? Unigram distribution.
ex) 단어들이 실제로 corpus에서 얼마나 등장했는가 확률 $U(w)$에 기반하여, $P(W) = U(w)^{3/4}/Z$ 확률분포에 기반해 negative sampling을 진행한다. 이렇게 설정할 경우 common, rare word 간의 차이를 다소 감소시킬 수 있음. less frequent words의 등장 확률을 다소 올릴 수 있다.
4. Why not capture Co-Occurrence Counts Directly?
왜 단어 동시 등장 확률을 바로 사용하지 않을까? 단어 동시등장 matrix를 만드는데에는 2가지 방식이 존재한다.
(1) Window based Co-occurrence Matrix
- Word2Vec과 유사하게, 각 단어 주변의 window를 활용함. -> semantic information을 반영함.
- I like deep learning, I like NLP, I enjoy flying이라는 corpus가 존재할 때, window length = 1인 co-occurence matrix는 다음과 같다. 또한 단어 등장 순서와 관계없이 구성하므로 symmetric하다.

- 위의 row/column vector를 단어 vector로 활용할 수 있다.
(2) Full Document Co-occurrence Matrix
- document는 일반적으로 구조를 가지고 있기 때문에 전반적인 topic에 대한 정보를 보존하고 있을 것.
- 따라서 주로 information retrieval / latent semantic analysis 등에 사용됨.
Problems of Co-occurrence Matrix
- Huge & Sparse
- Very High-dimensional : vocabulary size가 커지면 vector의 size가 같이 커짐. 많은 storage가 필요함.
- Sparsity : 매우 sparse한 vector가 되기 때문에 이후 classification 등을 수행할 때 sparsity issue로 robust하지 않은 Model을 만들게 될 가능성이 존재.
- Low-dimensional vectors
- 위 문제에 대한 해결방안으로, "대부분"의 중요한 정보들을 고정된, 저차원의 dimension에 Dense Vector로 저장하는 방법을 생각함.
- word2vec과 유사하게 보통 25-1000 dimension를 사용.
- 그렇다면, 어떻게 차원을 축소할 것인가?
SVD(Singular Vector Decomposition) : Dimensionality Reduction on X
- Co-occurrence Matrix에 대해 SVD를 진행하여 $X = U\Sigma V^T$ 형태로 분해.

- 그냥 raw count co-occurrence matrix에 적용할 경우 매우 poor한 결과를 얻게 될 것. SVD의 가정을 확인해 보면 Normaly distributed 가정이 필요하지만, co-occurrence matrix는 전혀 그렇지 않기 때문.
- 따라서, cell 내의 counts를 scaling하면 매우 도움이 됨. ex) log frequency, min(X, t), or Ignore function words
GloVe
- Idea : linear algebra based mathods와 neural update algorithm을 결합해서 만들어진 방법론.
- Linear Algebra Based Methods : LSA, HAL, COALS, Hellinger-PCA
- Neural Models : Skip-gram/CBOW, NNLM, HLBL, RNN

1. 원리 ) Co-occurrence Matrix와 Word Vectors를 활용해 Meaning Components Encoding
- Co-occurrence "확률값"을 사용해서 meaning components를 표현할 수 있다. => vector space 내에서 addition / subtraction을 활용해 의미론적 유사성/차이를 표현할 수 있음. (ex - queen -> king)
- ice와의 관계를 포함한 상태로 encoding을 얻고 싶다. 또한 gas -> solid의 의미론적 유사성/차이도 내포하고 싶을 때 아래와 같이 "Ratio"를 활용할 수 있음. 아래와 같이 (ice, steam)과 모두 관련이 있는 단어나 모두 관련이 없는 단어는 1에 가깝고, 한 단어에만 관련이 있을 경우 1에서 멀어진 값을 가지게 됨. 이렇게 단어간의 관계를 "linear" 하다고 볼 수 있다고 판단 가능.

- Q) 어떻게 하면 co-occurrence 확률값의 ratio를 word vector space 하의 Linear meaning component로써 활용해 볼 수 있을까?
- A ) 동시 등장 확률을 단어 벡터의 내적으로 표현해보자!
A: Log-bilinear model: $\quad w_i \cdot w_j=\log P(i \mid j)$
with vector differences $\quad w_x \cdot\left(w_a-w_b\right)=\log \frac{P(x \mid a)}{P(x \mid b)}$
2. Combining the best of both worlds GloVe
Explicit Loss function : $J=\sum_{i, j=1}^V f\left(X_{i j}\right)\left(w_i^T \tilde{w}_j+b_i+\tilde{b}_j-\log X_{i j}\right)^2$
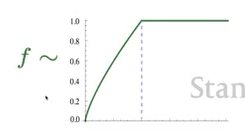
- 즉, Neural Model로부터 얻은 단어 임베딩 간의 내적($\left(X_{i j}\right)\left(w_i^T \tilde{w}_j$)이 log를 취한 co-occurrence( $\log X_{i j}$ )과 유사하도록 규정한 loss.
- 이때 함수 f : 빈번히 등장하는 단어가 지배적이지 않도록 자주 등장하는 단어는 f 함수로 일정 빈도 이상 등장하는 단어에 대해서는 동일한 가중치를 부여해 단어 빈도에 지나치게 영향을 받지 않도록 함. (더 드물게 등장하는 단어 조합에 집중하기 위해서)
- 이렇게 하면 (1) Fast Training (2) Scalable to huge corpora (3) small corpus, small vectors에서도 좋은 performance
How to Evaluate word vectors?
- Intrinsic VS Extrinsic
- Extrinsic
- 실제 task에 대해 Evaluation을 진행함. (web search, machine translation...)
- 장점 ) 실제 유의미한 실험을 진행
- 단점 ) 실제 성능 평가지표를 계산하기 위해 매우 오랜 시간이 걸릴 수 있음. / 다른 subsystem과 연관이 있을 때 단순히 word vector가 문제인지, 혹은 다른 component가 예전 word vector와 더 잘 맞았는지 등 이를 정의하기 쉽지 않음.
- Intrinsic :
- 특정/중간 subtask에 대해 Evaluation을 진행하기 때문에 word vector score 등을 계산 가능함.
- 장점 ) Fast to compute / component나 system을 이해하는데 도움이 됨.
- 단점 ) specific task만 대상으로 하기 때문에 실제 응용에서 모델의 성능을 제대로 반영하는가는 의문.
- ex) word vector analogies : man:woman 간의 관계로 king:queen 도출가능한가.
addition/subtraction 한 뒤의 word vector 간의 cosine distance(평가지표)를 기준으로 semantic, syntactic 정보를 포함하고 있는지 word vector 평가를 진행할 수 있음. - Problem) information이 존재하지만 선형적이지 않다면 어떻게 그를 평가할 것인가?

'NLP' 카테고리의 다른 글
| [Day3] 한권으로 끝내는 실전 LLM 파인튜닝 - 멀티헤드 어텐션과 피드포워드 (4) | 2025.01.03 |
|---|---|
| [CS224N] Lecture 5: Recurrent Neural Networks RNNs (2) | 2024.04.21 |
| Subword Tokenizer - BPE, WordPiece (0) | 2022.05.29 |
| An End-to-End Trainable Neural Network for Image-based Sequence Recognition and Its Application to Scene Text Recognition (1) | 2022.04.17 |
| StarSpace (3) | 2022.04.17 |



