다음은 [밑바닥부터 시작하는 딥러닝2]을 학습하고 정리하는 내용입니다. 신경망 기초 및 NLP 기초를 Numpy와 Matplotlib만 가지고 구현해봄으로써 자연어처리 및 딥러닝 구조에 대해 더 깊게 이해할 수 있기를 바랍니다.
1.1 수학과 파이썬 복습
1.1.1 벡터와 행렬
- Vector : 크기와 방향을 가진 양. 파이썬에서는 1차원 배열로 취급
- Matrix(행렬) : 2차원 형태의 배열.
- 수학에서는 열벡터가 기본이지만, 여기에서는 개발의 편의성을 위해 기본적으로 행벡터 기준으로 다룬다.
1.1.2 행렬의 원소별 연산
- Element-wise(원소별) 연산 : 다차원 넘파이 배열의 사칙연산 중 +와 *(원소별 원소 곱셈)가 가능.
1.1.3 브로드캐스트
- 넘파이의 다차원 배열에서는 형상(shape)가 다른 배열끼리도 연산이 가능하다. 아래처럼 $2 \times 2$ 행렬 A에 대해 1차원 배열 b를 곱할 경우 1차원 배열 b가 A와 형상이 같아지도록 확장된다. 이를 Broadcast라 한다.
A = np.array([[1,2],[3,4]])
b = np.array([10, 20])
A * b
# array([[10, 40],
# [30, 80]])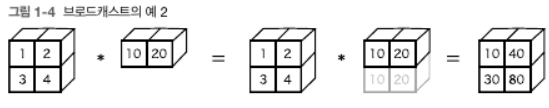
1.1.4 벡터의 내적과 행렬의 곱
- 내적(inner product) : $ \boldsymbol{ x } \cdot \boldsymbol{ y }= x_1 y_1 + x_2 y_2 + \cdots + x_n y_n$
- 행렬곱(matrix multiplication) : $ AB = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} e & f \\ g & h \end{bmatrix} = \begin{bmatrix} ae+bg & af+bh \\ ce+dg & cf+dh \\ \end{bmatrix}$
- Numpy의 np.dot()과 np.matmul() 메서드를 이용해서 구현 가능하다.
# 벡터의 내적
a = np.array([1, 2, 3]); b = np.array([4, 5, 6])
np.dot(a, b) # 32
# 행렬의 곱
A = np.array([[1, 2], [3, 4]]); B = np.array([[5, 6],[7,8]])
np.matmul(A, B)
# array([[19, 22],
# [43, 50]])1.1.5 행렬 형상 확인
- 행렬/벡터를 사용할 때는 반드시 그 shape(형상)을 주의해야 함. 수학적으로는 행렬의 곱에서는 대응하는 차언의 원소 수를 일치시켜야 한다. 즉, A의 열과 B의 행의 차수가 같아야 하고, 최종 곱셈인 C의 형태는 A의 행 x B의 열 형태의 차수를 가지게 된다.

1.2 신경망의 추론
1.2.1 신경망 추론 전체 그림
- 신경망은 입력을 출력으로 변환하는 함수라고 볼 수 있다.
- 입력층(Input Layer) : 2 뉴런, 은닉층(Hidden Layer) : 4 뉴런, 출력층(Output Layer) : 3 뉴런.
각 화살표에는 가중치(weight)가 존재하여 가중치 x 뉴런의 값의 합에 활성화 함수를 적용한 값 + 편향(bias)을 다음 뉴런의 입력값으로 활용한다. 아래 그림의 경우 모든 뉴런과 연결되어 있기 때문에 Fully Connected Layer라 한다.
수식 : $h_i = x_1 w_{1i} + x_2 w_{2i} + b_i$, 행렬곱을 이용하면 깔끔하게 정리 가능하다.
$\left(h_1, h_2, h_3, h_4\right)=\left(x_1, x_2\right)\left(\begin{array}{llll}w_{11} & w_{12} & w_{13} & w_{14} \\ w_{21} & w_{22} & w_{23} & w_{24}\end{array}\right)+\left(b_1, b_2, b_3, b_4\right)$
$\rightarrow \boldsymbol{h} = \boldsymbol{x} W + \boldsymbol{b} $

- Minibatch의 경우 : vector(or matrix) $\boldsymbol{x}$의 행 각각에 샘플 데이터가 하나씩 저장됨. 아래와 같이 각 미니배치가 올바르게 변환되었는지를 파악하고, N개의 sample data가 한꺼번에 Fully connected layer를 통해 변환되며 은닉층도 N개의 뉴런이 함께 계산된다.

- 비선형 활성화 함수(non-linear activation function)을 이용해 신경망의 표현력을 높일 수 있다. 대표적으로 사용하는 비선형 활성화 함수 : Sigmoid(시그모이드), ReLU, LeakyReLU, etc
- Sigmoid : $\sigma(x) = \frac{1}{1+exp(-x)}$, $x \in \mathbb{R} \rightarrow 0 \leq \sigma(x) \leq 1 $
- 이후, 활성화 함수의 출력인 $a$를 또 다른 완전연결계층(가중치 행렬 4 x 3)에 통과시켜 다시 변환한다. 최종 출력인 s의 형상은 (10, 3)이 된다. 즉, 10개의 데이터가 한꺼번에 각각 3차원 데이터로 변환되었다는 뜻이다.
def sigmoid(x):
return 1 / (1 + np.exp(-x))
x = np.random.randn(10, 2) # 입력 (N x 2)
W1 = np.random.randn(2, 4) # 가중치
b1 = np.random.randn(4) # 편향
W2 = np.random.randn(4, 3) # 가중치
b2 = np.random.randn(3) # 편향
h = np.matmul(x, W1) + b1
a = sigmoid(h) # sigmoid activation fuction
s = np.matmul(a, W2) + b2 # 최종 output1.2.2 계층으로 클래스화 및 순전파 구현
- 신경망에서 하는 처리를 Layer(계층)로 구현해보자. 신경망 추론(inference) 과정에서 하는 처리를 신경망의 순전파(forward)라 한다. 이후 신경망 학습 과정에서는 데이터를 반대방향으로 전파하기 때문에 역전파(backward propagation)이라 부른다.
- 신경망의 다양한 계층을 다음 규칙에 따라 모듈화.
(1) 모든 계층은 forward()와 backward() 메서드를 가진다.
(2) 모든 계층은 인스턴스 변수인 params와 grads를 가진다. (params : 가중치, 편향 등 매개변수 담는 list, grads : params에 저장된 각 매개변수에 대응하며, 해당 매개변수의 기울기를 보관하는 리스트.) - Sigmoid Layer & Affine Layer :
class Sigmoid:
def __init__(self):
self.params = [] # 학습하는 매개변수가 없으므로 빈 리스트로 초기화
def forward(self, x):
return 1 / (1 + np.exp(-x))
class Affine:
def __init__(self, W, b):
self.params = [W, b]
def forward(self, x):
W, b = self.params
out = np.matmul(x, W) + b
return out- 위의 계층을 사용해 신경망의 추론 처리를 구현해보자.

class TwoLayerNet:
def __init__(self, input_size, hidden_size, output_size):
I, H, O = input_size, hidden_size, output_size
# 가중치와 편향 초기화
W1 = np.random.randn(I, H)
b1 = np.random.randn(H)
W2 = np.random.randn(H, O)
b2 = np.random.randn(O)
# 계층 생성
self.layers = [
Affine(W1, b1),
Sigmoid(),
Affine(W2, b2)
]
# 모든 가중치를 리스트에 모은다.
self.params = []
for layer in self.layers:
self.params += layer.params
def predict(self, x):
for layer in self.layers:
x = layer.forward(x)
return x
x = np.random.randn(10, 2)
model = TwoLayerNet(2, 4, 3)
s = model.predict(x)- (1) 초기화 메서드(__init__) : 가중치를 초기화하고 3개의 계층을 생성한다. 마지막으로는 학습해야 할 가중치 매개변수들을 params 리스트에 모아 저장한다.
- 학습해야 할 모든 매개변수가 model, params라는 하나의 리스트에 모여있으므로, 신경망 학습이 한 층 수월해진다.
1.3 신경망의 학습
1.3.1 손실 함수
- 손실(Loss) : 학습 단계의 특정 시점에서 신경망의 성능을 나타내는 척도. 학습시 주어진 정답과 신경망이 예측한 결과를 비교해 예측이 얼마나 나쁜가를 산출한 단일 값(scala)이다.
- 다중 클래스 분류 신경망에서는 흔히 교차 엔트로피 오차(Cross Entropy Error)를 이용함. 지금까지 봐온 예제로 손실을 구해보자.

- 앞 절의 Layer 마지막 단계에 Softmax 계층(softmax 함수)과 Cross Entropy Error 계층을 새로 추가하자. Softmax 계층의 출력은 확률이 되어 마지막 cross entropy error 계층에는 확률값과 정답 label이 입력된다.
- Softmax function : $y_k = \frac{exp(s_k)}{\sum_{i=1}^{n} exp(s_i)}$. 즉, 출력이(class가) 총 $n$개 일 때, $y_k$는 $k$번째 class에 해당하는 softmax 함수의 출력이다.
- 소프트맥스 함수의 출력의 각 원소는 0.0 이상, 1.0 이하의 실수이며 이 원소들을 모두 더하면 1이 된다. ('확률'로 해석 가능). 소프트맥스의 출력인 이 '확률'이 다음 차례인 교차 엔트로피 오차에 입력된다.
- Cross Entropy Error : $L = - \sum_{k} t_k log y_k $, $t_k$는 k번째 클래스에 해당하는 정답 레이블이며 원-핫 벡터로 표기한다. 따라서 위의 식은 실질적으로 정답 label이 1인 원소에 해당하는 출력의 log를 계산할 뿐이다.
- 미니배치 처리를 고려하면, 교차 엔트로피 오차의 식은 다음과 같다. N으로 나눠서 평균 손실 함수를 구함으로써 미니배치의 크기에 관계없이 일관된 척도를 얻을 수 있다. :
$$L = -\frac{1}{N} \sum_{n} \sum_{k} t_{nk} log y_{nk} $$ where $t_{nk}$ : $n$번째 데이터의 $k$차원째의 값이자 정답 label, $y_{nk}$ : 신경망의 출력
def softmax(x):
if x.ndim == 2:
x = x - x.max(axis=1, keepdims=True)
x = np.exp(x)
x /= x.sum(axis=1, keepdims=True)
elif x.ndim == 1:
x = x - np.max(x)
x = np.exp(x) / np.sum(np.exp(x))
return x
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
if t.size == y.size:
t = t.argmax(axis=1)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
class SoftmaxWithLoss:
def __init__(self):
self.params, self.grads = [], []
self.y = None
self.t = None
def forward(self, x, t):
self.t = t
self.y = softmax(x)
if self.t.size == self.y.size:
self.t = self.t.argmax(axis=1)
loss = cross_entropy_error(self.y, self.t)
return loss1.3.2 미분과 기울기
- 신경망 학습의 목표 : 손실을 최소화하는 매개변수를 찾는것. 이때 중요한 것이 '미분'과 '기울기'이다.
- $y = f(x)$에 대해 $\frac{dy}{dx}$ 미분의 의미 : $x$의 값을 매우 조금 변화시켰을 때 $y$값이 얼마나 변하는가의 '변화의 정도'를 의미한다. 또한 각 $x$에서의 '기울기'에 해당한다.
- 다변수 미분 : $L = f(x)$에 대해 $$\frac{\partial L}{\partial \mathbf{x}}=\left(\frac{\partial L}{\partial x_1}, \frac{\partial L}{\partial x_2}, \cdots, \frac{\partial L}{\partial x_n}\right)$$
- 이처럼 벡터의 각 원소에 대한 미분을 정리한 것이 기울기(gradient)이다.
- 행렬 미분 : $L = f(\mathbf{W})$에 대해 $$\frac{\partial L}{\partial \mathbf{W}}=\left(\begin{array}{ccc}\frac{\partial L}{\partial W_{11}} & \cdots & \frac{\partial L}{\partial W_{1 n}} \\ \vdots & \ddots & \\ \frac{\partial L}{\partial W_{m 11}} & & \frac{\partial L}{\partial W_{m m}}\end{array}\right)$$
- 중요한 점은 $\mathbf{W}$와 $ \frac{\partial L}{\partial \mathbf{W}}$의 형상(shape)이 같다는 점이며, 이를 이용하면 Chain rule을 사용해 매개변수 갱신과 연쇄 법칙을 쉽게 구현 가능하다.
1.3.3 연쇄 법칙(Chain Rule)
- 각 매개변수(W1, b1, W2, b2)에 대한 손실의 기울기를 얻기 위해 오차역전파(Back-Propagation)을 활용할 수 있다.
- 연쇄 법칙(Chain Rule) : 합성함수에 대한 미분법칙으로써, $y = f(x), z = g(y) = g(f(x))$에 대해 $ \frac{\partial z}{\partial x} = \frac{\partial z}{\partial y} \frac{\partial y}{\partial x} $로 합성함수의 미분을 계산할 수 있다.
- 즉, 아무리 여러개의 함수를 연결해도, 그 미분은 개별 함수의 미분들의 곱으로 계산가능하다는 의미이다.
1.3.4 계산 그래프

- 순전파(forward propagation) : 어떤 계산을 거쳐서 최종적으로 scalar $L$이 출력된다고 가정하자. 현재 목표는 $L$의 미분(기울기)을 각 변수에 대해 구하는 것이다.
- 역전파(backward propagation) : 역전파에서 '전파되는 값'은 최종 출력 scalar $L$의 각 변수에 대한 미분이다. 즉, $z$에 대한 미분은 \frac{\partial L}{\partial z} $이며 $x, y$에 대한 미분은 각각 $ \frac{\partial L}{\partial x}, \frac{\partial L}{\partial y} $이다.
- 연쇄법칙에 따라, 역전파로 흐르는 미분값은 상류로부터 흘러온 미분과, 각 연산 노드의 국소 미분을 곱해 계산할 수 있다. $\rightarrow \frac{\partial L}{\partial x} = \frac{\partial L}{\partial z} \frac{\partial z}{\partial x}, \frac{\partial L}{\partial y} = \frac{\partial L}{\partial z} \frac{\partial z}{\partial y} $.
- 만약 벡터나 행렬 혹은 텐서같은 다변수를 흘릴 경우 각 원소를 독립적으로 계산하는 "원소 별 연산"을 수행한다.
- 덧셈 노드, 곱셈 노드, 분기 노드, Repeat 노드, Sum 노드, etc

- Repeat 노드 : 2개로 분기하는 분기 노드를 일반화하면 N개로의 분기(복제)가 된다.
- 길이가 D인 배열을 N개로 복제할 경우, 그 역전파는 N개의 기울기를 모두 더해 구할 수 있다.
- y = np.repeat(x, N, axis=0) # 순전파, 원소 복제를 실행
- dx = np.sum(dy, axis=0, keepdims=True) # 역전파

- Sum 노드 : $N \times D$ 배열에 대해 그 총합을 0 축에 대해 구하는 계산.
- 역전파 시 상류로부터의 기울기를 모든 화살표에 분배한다.
- y = np.sum(x, axis=0, keepdims=True) # 순전파
- dx = np.repeat(dy, N, axis=0) # 역전파
- Sum 노드와 Repeat 노드는 서로 반대관계이다. Sum 노드의 순전파가 Repeat 노드의 역전파가 되며, Repeat 노드의 순전파가 Sum 노드의 역전파가 된다.
- MatMul 노드 (행렬곱) : $\mathbf{y} = \mathbf{xW}$, $\mathbf{x}, \mathbf{W}, \mathbf{y}$의 형상은 각각 $1 \times D, D \times H, 1 \times H$.
- $\mathbf{x}$의 $i$번째 원소에 대한 미분 : $$ \frac{\partial L}{\partial x_i} = \sum_{j} \frac{\partial L}{\partial y_j} \frac{\partial y_j}{\partial x_i} = \sum_{j} \frac{\partial L}{\partial y_j} W_{ij} $$ since $ \frac{\partial y_j}{\partial x_i} = W_{ij}$
$$\rightarrow \frac{\partial L}{\partial \mathbf{x}} = \frac{\partial L}{\partial \mathbf{y}} \mathbf{W}^T$$

class MatMul:
def __init__(self, W):
self.params = [W] # 학습하는 매개변수를 params에 보관
self.grads = [np.zeros_like(W)] # 매개변수에 대응되는 기울기를 보관
self.x = None
def forward(self, x):
W, = self.params
out = np.matmul(x, W)
self.x = x
return out
def backward(self, dout):
W, = self.params
dx = np.matmul(dout, W.T)
dW = np.matmul(self.x.T, dout)
self.grads[0][...] = dW # 가중치의 기울기를 grads에 저장
# [...] : 넘파이 배열이 가리키는 메모리 위치를 고정시킨 다음 그 위치에 원소들을 덮어쓴다. (deep copy)
return dx1.3.5 기울기 도출과 역전파 구현
- Sigmoid 계층 : $y = \frac{1}{1+exp(-x)} \rightarrow \frac{\partial y}{\partial x} = y (1-y)$.
따라서, $\frac{\partial L}{\partial x} = \frac{\partial L}{\partial y} y (1-y) $로 계산 가능. - Affile 계층 : bias를 더할 때 넘파이의 브로드캐스트가 사용되어 아래 그림과 같이 표기 가능.

- Softmax with Loss 계층 : softmax 계층의 역전파가 $(y_i - t_i)$로 깔끔하게 떨어진다. 즉, 역전파 값이 자신의 출력과 정답 레이블의 차이!

class Sigmoid:
def __init__(self):
self.params, self.grads = [], []
self.out = None # 출력
def forward(self, x):
out = 1 / (1 + np.exp(-x))
self.out = out # 순전파 때는 출력을 out에 저장
return out
def backward(self, dout):
dx = dout * (1.0 - self.out) * self.out # 역전파시 out 변수를 사용
return dx
class Affine:
def __init__(self, W, b):
self.params = [W, b] # 매개변수 저장
self.grads = [np.zeros_like(W), np.zeros_like(b)] # 기울기 저장
self.x = None
def forward(self, x):
W, b = self.params
out = np.matmul(x, W) + b
self.x = x
return out
def backward(self, dout):
W, b = self.params
dx = np.matmul(dout, W.T)
dW = np.matmul(self.x.T, dout)
db = np.sum(dout, axis=0)
self.grads[0][...] = dW # 가중치 매개변수 기울기를 인스턴스 변수 grads에 저장
self.grads[1][...] = db
return dx
class SoftmaxWithLoss:
def __init__(self):
self.params, self.grads = [], []
self.y = None
self.t = None
def forward(self, x, t):
self.t = t
self.y = softmax(x)
if self.t.size == self.y.size:
self.t = self.t.argmax(axis=1)
loss = cross_entropy_error(self.y, self.t)
return loss
def backward(self, dout=1):
batch_size = self.t.shape[0]
dx = self.y.copy()
dx[np.arange(batch_size), self.t] -= 1
dx *= dout
dx = dx / batch_size
return dx1.3.6 가중치 갱신
- 신경망의 학습 순서 :
1단계 : 미니배치 - 훈련 데이터 중 무작위로 다수의 데이터를 골라낸다.
2단계 : 기울기 계산 - 오차역전파법으로 각 가중치 매개변수에 대한 손실함수의 기울기를 구한다.
3단계 : 매개변수 갱신 - 기울기를 사용하여 가중치 매개변수를 갱신한다.
4단계 : 반복 - 1~3단계를 필요한 만큼 반복한다. - 경사하강법(Gradient Descent) : 기울기는 현재의 가중치 매개변수에서 손실을 가장 크게 하는 방향을 가리키기 때문에 매개변수를 이 기울기와 반대 방향으로 갱신하면 손실을 줄일 수 있다.
- 확률적 경사하강법(Stochastic Gradient Descent, SGD) : (현재의) 가중치를 기울기 방향으로 일정 거리만큼 갱신한다.
$$\mathbf{W} \leftarrow \mathbf{W} - \eta \frac{\partial L}{\partial \mathbf{W}}$$. - 이외에도 Momentum, AdaGrad, Adam 등의 기법을 활용할 수 있다.
class SGD:
def __init__(self, lr=0.01):
self.lr = lr
def update(self, params, grads):
for i in range(len(params)):
params[i] -= self.lr * grads[i]1.4 신경망으로 문제를 풀다
1.4.2 신경망 구현
class TwoLayerNet:
def __init__(self, input_size, hidden_size, output_size): # 입력층, 은닉층, 출력층 뉴런 수를 입력으로 받음.
I, H, O = input_size, hidden_size, output_size
# 가중치, 편향 초기화
W1 = 0.01 * np.random.randn(I, H) # 가중치 : 작은 무작위 값으로 초기화
b1 = np.zeros(H) # 편향 : 0 벡터로 초기화
W2 = 0.01 * np.random.randn(H, O)
b2 = np.zeros(O)
# Layer 생성 - 필요한 계층을 생성해 모아두기
self.layers = [
Affine(W1, b1),
Sigmoid(),
Affine(W2, b2)
]
self.loss_layer = SoftmaxWithLoss()
# 모든 가중치와 기울기를 리스트에 모은다.
self.params, self.grads = [], []
for layer in self.layers:
self.params += layer.params # 모델에서 사용하는 매개변수 모아두기
self.grads += layer.grads # 모델에서 사용하는 가중치 모아두기
# 추론 함수
def predict(self, x):
for layer in self.layers:
x = layer.forward(x)
return x
# 순전파 함수
def forward(self, x, t):
score = self.predict(x)
loss = self.loss_layer.forward(score, t)
return loss
# 역전파 함수
def backward(self, dout=1):
dout = self.loss_layer.backward(dout)
for layer in self.layers[::-1]:
dout = layer.backward(dout)
return dout1.4.3 학습용 코드
- 학습 데이터와 신경망 (모델)과 옵티마이저(SGD 최적화기)를 생성하고, 앞 절에서 설명한 4 단계의 절차대로 학습을 수행한다.
# 1. hyperparameter 설정 - 학습 에폭 수, 미니배치 크기, 은닉층의 뉴런 수, 학습률 등을 술정한다.
max_epoch = 300
batch_size = 30
hidden_size = 10
learning_rate = 1.0
# 2. 데이터 준비, 모델과 옵티마이저 생성
x, t = load_data()
model = TwoLayerNet(input_size=2, hidden_size=hidden_size, output_size=3)
optimizer = SGD(lr=learning_rate)
# 학습에 사용하는 변수
data_size = len(x)
max_iters = data_size // batch_size
total_loss = 0
loss_count = 0
loss_list = []
for epoch in range(max_epoch):
# 3. data 뒤섞어주기 - epoch마다
idx = np.random.permutation(data_size)
x = x[idx]; t = t[idx]
for iters in range(max_iters):
# 학습은 minibatch 방식으로 진행되며, 데이터를 무작위로 선택했다.
batch_x = x[iters*batch_size:(iters+1)*batch_size]
batch_t = t[iters*batch_size:(iters+1)*batch_size]
# 4. 기울기를 구해 매개변수 갱신
loss = model.forward(batch_x, batch_t)
model.backward()
optimizer.update(model.params, model.grads)
total_loss += loss
loss_count += 1
# 5. 학습 결과 정기적 출력
if (iters+1) % 10 == 0:
avg_loss = total_loss / loss_count
print('| 에폭 %d | 손실 %.2f' % (epoch+1, avg_loss))
loss_list.append(avg_loss)
total_loss, loss_count = 0, 0- 결과를 그려보면 손실 값이 학습이 진행될수록 낮아지는 것을 볼 수 있다.
- 학습된 신경망은 깊은 은닉층을 추가하고 비선형 activation 함수를 활용함으로써 나선형 패턴을 올바르게 파악해 비선형 분리 영역을 학습가능하다.

1.5 계산 고속화
- 신경망 고속화에 도움이 되는 '비트 정밀도'와 'GPU'
1.5.1 비트 정밀도
- Numpy 부동소수점 수는 64 bit data type(float64)을 기본으로 함.
- 신경망 추론/학습은 32bit 부동소수점 수로도 문제 없이 수행할 수 있기 때문에 메모리 관점에서는 32bit가 더 나음.
- 신경망 계산 시 데이터를 전송하는 '버스 대역폭'이 병목이 되는 경우가 많은데, 이 경우도 작은 테이터타입이 더 유리
- 계산 속도 측면에서도 32bit 부동소수점 수가 일반적으로 더 빠르다.
- 신경망 추론으로 한정 시 16 bit 부동소수점 수를 사용해도 인식률이 거의 떨어지지 않음.
1.5.2 GPU(쿠파이)
- cupy라는 엔비디아 GPU를 사용해 병렬 계산이 가능판 패키지가 존재.
1.6 정리
- 신경망은 입력층, 은닉층(중간층), 출력층을 지닌다.
- 완전연결계층에 의해 선형 변환이 이뤄지고, 활성화 함수에 의해 비선형 변환이 이뤄진다.
- 완전연결계층이나 미니배치 처리는 행렬로 모아 한꺼번에 계산할 수 있다.
- 오차역전파법을 사용하여 신경망의 손실에 관한 기울기를 효율적으로 구할 수 있다.
- 신경망이 수행하는 처리는 계산 그래프로 시각화 할 수 있으며, 순전파와 역전파를 이해하는데 도움이 된다.
- 신경망의 구성 요소들을 '계층'으로 모듈화해두면, 이를 조립하여 신경망을 쉽게 구성할 수 있다.
- 신경망 고속화에는 GPU를 이용한 병렬 계산과 데이터의 비트 정밀도가 중요하다.
'Deep Learning' 카테고리의 다른 글
| [밑바닥부터 시작하는 딥러닝2] Chapter 4. Word2Vec 속도 개선 (0) | 2024.07.08 |
|---|---|
| [밑바닥부터 시작하는 딥러닝2] Chapter 3. Word2Vec (0) | 2024.07.02 |
| [밑바닥부터 시작하는 딥러닝2] Chapter 2. 자연어와 단어의 분산 표현 (0) | 2024.06.24 |
| Gradient Descent (0) | 2022.06.26 |
| Neural Networks and Deep Learning - Logistic Regression (0) | 2022.06.19 |



